问题概述
有n个资产,其风险可用方差 $ \sigma_i^2 $ 衡量,收益率可用期望(历史均值) $ R_i $ 衡量,n个资产价格的变动可能存在联动关系,用协方差 $ cov_{i,j} $ 衡量,其中 $ cov_{i,i}=\sigma_i^2 $ 。
现在同时投资这n个资产,以 $ w_i $ 的权重分配第i个资产($ w_i\in(-\infty, +\infty) $,负数代表做空),构建出一个投资组合(Portfolio)。于是可以求出这个组合的收益率和方差如下。
$$R_p=\sum_{i}w_i*R_i$$
$$\sigma_p^2=\sum_{i}\sum_{j}w_i*w_j*cov_{i,j}$$
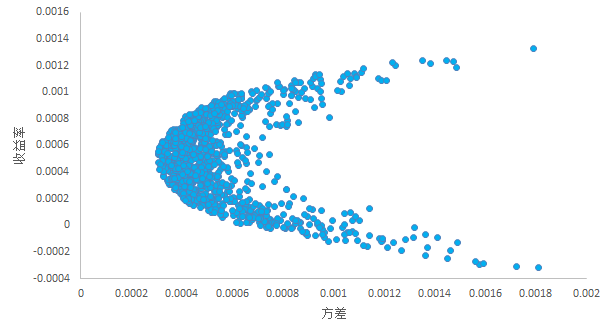
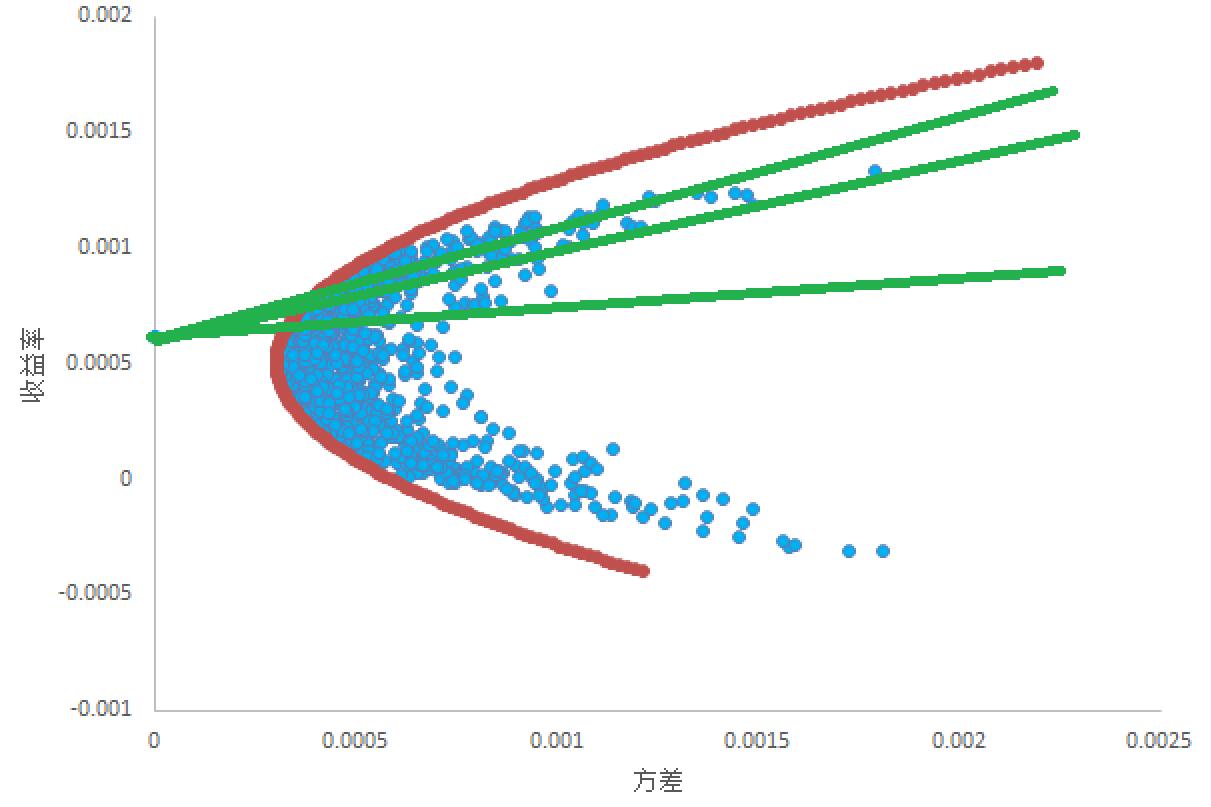
现在随机生成n组 $ w_i $ ,可以得到n个 $ (R_p, \sigma_p^2) $ ,以收益率和方差为横纵坐标轴,可以把生成的n个坐标点绘制成图,如下所示。
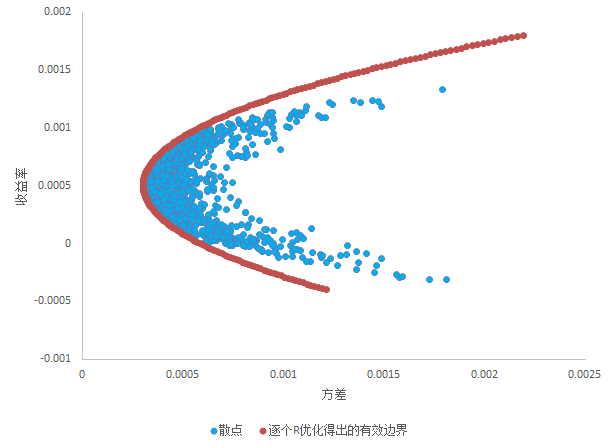
可以看出,散点看起来似乎有一个边界,这个边界即为“有效边界”(边界之外的组合无法用这n个资产构造出来)。现在我们需要把这个有效边界的函数解析式形式求出来,首先可以发现,有效边界实际上是在收益率确定为 $ R $ 的情况下,方差最小的点组成的,于是,这个问题就可以写成如下优化问题形式,其中 $ min $ 部分指所求最小方差, $ s.t. $ 部分表示变量约束条件。设定多个 $ R $ ,进行求解,即可得到多个 $ \sigma_p^2 $ ,生成一组 $ (R_p, \sigma_p^2) $ 散点,这些散点即为有效边界上的点,如图。
$$ \begin{equation}\begin{split}min\ \sigma_p^2=\sum_{i}\sum_{j}w_iw_j*cov_{i,j}\\s.t.\ \begin{cases}\sum_{i}w_i=1\\R_p=\sum_{i}w_i*R_i=R\end{cases}\end{split}\end{equation} $$
拉格朗日乘数法
经过上述步骤,有效边界的求解已经写成了一个带约束的优化问题的形式,而拉格朗日乘数法正好可用来求解此类问题。拉格朗日乘数法将优化问题转变为了解方程组。例如以下问题:
$$ \begin{equation}\begin{split}min\ f(x,y,z)\\s.t.\ \begin{cases}g(x,y,z)=0\\h(x,y,z)=0\\l(x,y,z)=0\end{cases}\end{split}\end{equation} $$
Lagrange乘数法的求解步骤是这样的:
首先,构造一个新的函数
$$ F(x,y,z,\lambda_1, \lambda_2, \lambda_3)=f(x,y,z)+\lambda_1*g(x,y,z)+\lambda_2*h(x,y,z)+\lambda_3*l(x,y,z) $$
分别求这个函数对所有自变量的偏导,令其等于0,得到如下方程组。
$$\begin{cases}\frac{dF}{dx}=0\\\frac{dF}{dy}=0\\\frac{dF}{dz}=0\\\frac{dF}{d\lambda_1}=0\\\frac{dF}{d\lambda_2}=0\\\frac{dF}{d\lambda_3}=0\end{cases}$$
接着解出一组 $ x,\ y,\ z $ ,代回 $ f(x,y,z) $ 即为最优解。
3个资产举例
考虑本篇文章的循序渐进性,先用Lagrange乘数法对3个资产的有效边界进行求解,之后再求解n个的,这样或许好理解些。
首先写出3个资产的最优化问题形式,同第一部分所提到的,3个资产的情况如下。
$$ \begin{equation}\begin{split}min\ \sigma_p^2=\sum_{i=1}^{3}\sum_{j=1}^{3}w_iw_j*cov_{i,j}\\s.t.\ \begin{cases}\sum_{i=1}^{3}w_i=1\\R_p=\sum_{i=1}^{3}w_i*R_i=R\end{cases}\end{split}\end{equation} $$
首先构造一个大函数,如下。
$$ F(w_1,w_2,w_3,\lambda_1,\lambda_2)=\sum_{i=1}^{3}\sum_{j=1}^{3}w_iw_j*cov_{i,j}+\lambda_1(\sum_{i=1}^{3}w_i-1)+\lambda_2(\sum_{i=1}^{3}w_i*R_i-R) $$
然后对每个自变量求偏导,并令其等于0,得到如下方程组。
$$\begin{cases}\frac{dF}{dw_1}=\sum_{j=1}^{3}w_1*cov_{1,j}+\lambda_1+\lambda_2*R_1=0\\\frac{dF}{dw_2}=\sum_{j=1}^{3}w_2*cov_{2,j}+\lambda_1+\lambda_2*R_2=0\\\frac{dF}{dw_3}=\sum_{j=1}^{3}w_3*cov_{3,j}+\lambda_1+\lambda_2*R_3=0\\\frac{dF}{d\lambda_1}=\sum_{i=1}^{3}w_i-1=0\\\frac{dF}{d\lambda_2}=\sum_{i=1}^{3}w_i*R_i-R=0\end{cases}$$
可以看出,方程组是线性的,可将其写成矩阵形式,如下。
$$\begin{bmatrix}cov_{1,1}&cov_{1,2}&cov_{1,3}&1&R_1\\cov_{2,1}&cov_{2,2}&cov_{2,3}&1&R_2\\cov_{3,1}&cov_{3,2}&cov_{3,3}&1&R_3\\1&1&1&0&0\\R_1&R_2&R_3&0&0\\\end{bmatrix}\begin{bmatrix}w_1\\w_2\\w_3\\\lambda_1\\\lambda_2\end{bmatrix}=\begin{bmatrix}0\\0\\0\\1\\R\\\end{bmatrix}$$
两边乘系数矩阵的逆,转变为如下形式。
$$\begin{bmatrix}w_1\\w_2\\w_3\\\lambda_1\\\lambda_2\end{bmatrix}=\begin{bmatrix}cov_{1,1}&cov_{1,2}&cov_{1,3}&1&R_1\\cov_{2,1}&cov_{2,2}&cov_{2,3}&1&R_2\\cov_{3,1}&cov_{3,2}&cov_{3,3}&1&R_3\\1&1&1&0&0\\R_1&R_2&R_3&0&0\\\end{bmatrix}^{-1}\begin{bmatrix}0\\0\\0\\1\\R\\\end{bmatrix}$$
通过观察可以发现,方程右边的变量只有 $ R $ ,且只出现在右下角,因此解出的 $ w_i $ 与 $ R $ 呈 $ w_i=a+b*R $ 的形式,代入$ \sigma_p^2=\sum_{i}\sum_{j}w_i*w_j*cov_{i,j} $,可以发现,$ \sigma_p^2 $ 与 $ R $ 呈现二次函数关系,由此即可得出 $ \sigma_p^2 $ 与 $ R $ 的解析式,即 $ \sigma_p^2=aR^2+bR+c $。
推广至n个资产
n个资产的推导在前期与3个资产一致,最后得到的方程组矩阵形式结果如下。
$$\begin{bmatrix}w_1\\\vdots\\w_n\\\lambda_1\\\lambda_2\end{bmatrix}=\begin{bmatrix}cov_{1,1}&\cdots&cov_{1,n}&1&R_1\\\vdots&\ddots&\vdots&\vdots&\vdots\\cov_{n,1}&\cdots&cov_{n,n}&1&R_n\\1&\cdots&1&0&0\\R_1&\cdots&R_n&0&0\\\end{bmatrix}^{-1}\begin{bmatrix}0\\\vdots\\0\\1\\R\\\end{bmatrix}$$
同样可以由此看出 $ w_i $ 与 $ R $ 呈 $ w_i=a+b*R $ 的形式,从而得到 $ \sigma_p^2=aR^2+bR+c $ 的结果。
附:在存在无风险资产下的情况下,有效边界为直线的理解
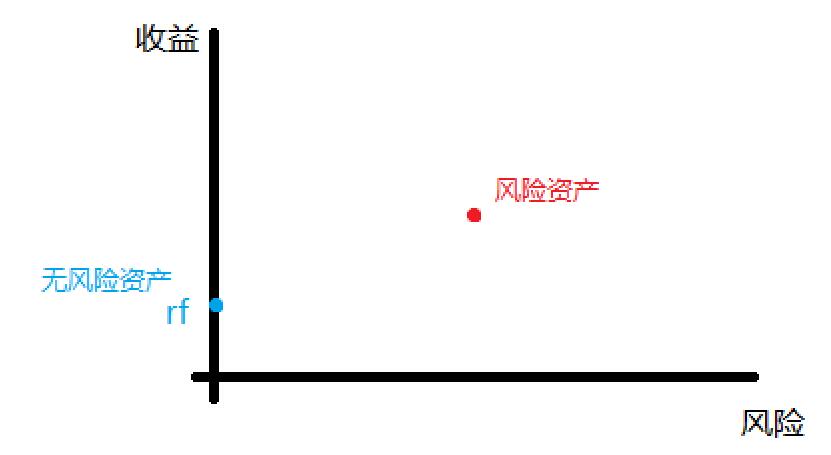
对于这种情况,我们可以把风险组合看作一个整体。首先我们考虑只有一个风险资产的情况:
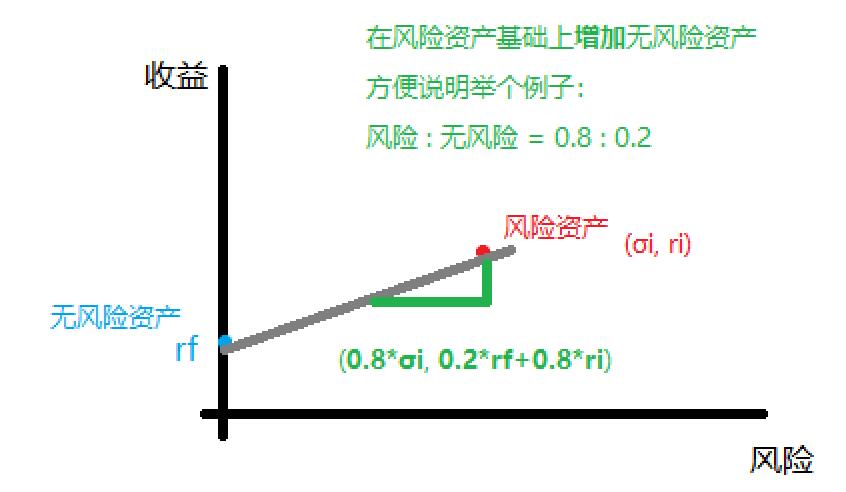
在风险资产的基础上增加无风险资产,方便说明举个例子:80%投资于风险资产,20%投资于无风险资产。新的资产组合点如下图所示。
我们放宽上面的例子,把80%换成 $ w_i $ ,可以得到那个绿色坐标:
$$ (w_i\sigma_i, (1-w_i)r_f+w_i r_i) $$
上面的坐标其实是个关于 $ w_i $ 的参数方程,可以写成下面形式。
$$ \begin{cases}x = w_i\sigma_i\\y = (1-w_i)r_f+w_i r_i\end{cases} $$
我们消去其中的 $ w_i $ 就能把y与x的表达式求出来啦,如下。
$$ y=r_f \left(1-\frac{x}{\sigma _i}\right)+\frac{x r_i}{\sigma _i} $$
化简得到。
$$ y=\frac{x \left(r_i-r_f\right)}{\sigma _i}+r_f $$
可以看到这就是一条直线,而且这条直线经过 $ (0, r_f) $ 和 $ (\sigma_i, r_i) $ 两个点,也就是图中一开始的两个点。
所以对于任意的一个无风险资产,和一个风险资产,我们都可以认为,它们的有效资产组合所有可能的情况,绘制在图中就是一条射线(风险不能为负数,所以是射线)。
那么,现在我们把前面推导的N个风险资产组合有效边界的结论结合一下。
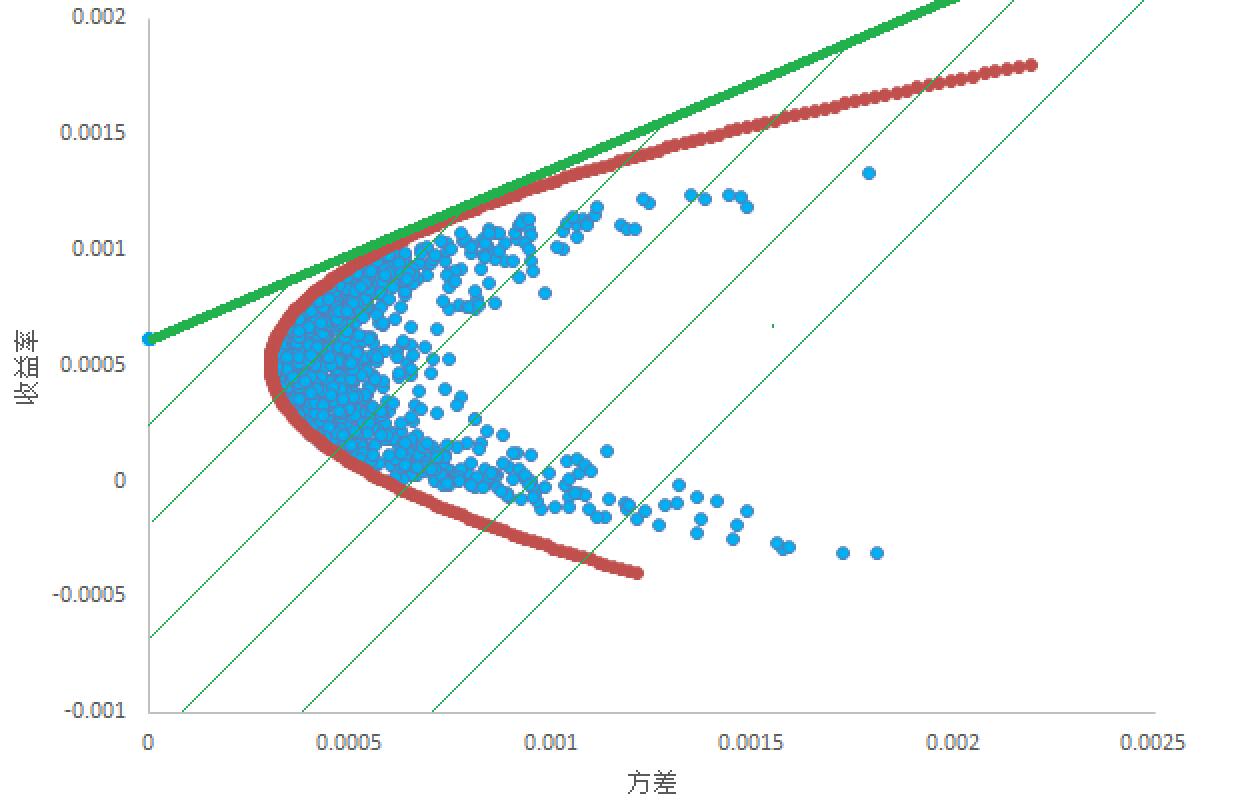
有N个风险资产组合,和一个无风险资产,如下图。
可以看到,这样可以组成无数条射线,但是总归还是有个边界,很容易可以想到,这个边界就是无风险资产所在的点,与抛物线的切线。如下图所示。
以上就是本人对在存在无风险资产下的情况下,有效边界为直线的理解啦!